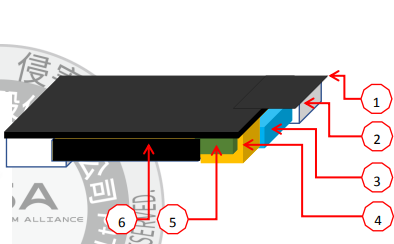
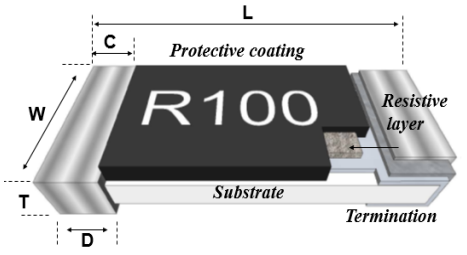
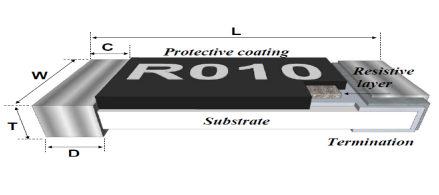
支路电流法的计算步骤用支路电流法计算电路的具体步骤为：1）首先，在电路图中标记每个支路电流的参考方向。
2）列出KCL方程。
一般来说，对于具有n个节点的电路，基尔霍夫（Kirchhoff）的现行定律只能获得（n-1）个独立的KCL方程。
3）列出独立的KVL方程。
独立KVL方程的数量是单孔电路的数量：b-（n-1）。
4）结合所有列出的公式来求解每个分支的电流，然后求解电路中的其他电压，功率等。
对于线性电路，当应用支路电流方法时，电路不能包含由压控组件组成的支路。
由于该分支的电压不能用电流表示，因此无法从KVL方程中消除该分支的电压。
此外，当电路（线性或非线性）包含仅由独立电流源组成的分支时，最好使用功率传输方法来传输电流源（请参阅电路转换），然后使用分支电流计算方法。
该算法的特点和优点：直观，您只需要支路电流即可。
缺点：当分支数很大时，变量很多并且求解过程很麻烦，因此手动计算是不合适的。
支路电流法的适用条件支路电流法以支路电流为求解对象，应用基尔霍夫定律为节点和回路写出所需的方程式，然后求解方程式以获得每个支路的电流，您可以使用欧姆定律获得每个分支上的电压值。
结论：对于具有b个分支，n个节点和m个网格的电路，应用KCL可以列出（n-1）个独立节点的当前方程，应用KVL可以列出m个网格电压方程，并且独立方程的总数为（n-1）+ m，它恰好等于分支数b，因此方程组具有唯一的解。
如图3-1所示，如果列出，则可以列出以下方程式：通过求解方程式可得到I1，I2和I3。
